Database of Experimental Results
SModelS stores all the information about the experimental results in the Database. Below we describe both the directory, object structure of the Database and how the information in stored in the database is used within SModelS.
Database: Directory Structure
The Database is organized as files in an ordinary (UNIX) directory hierarchy, with a thin Python layer serving as the access to the database. The overall structure of the directory hierarchy and its contents is depicted in the scheme below (click to enlarge):
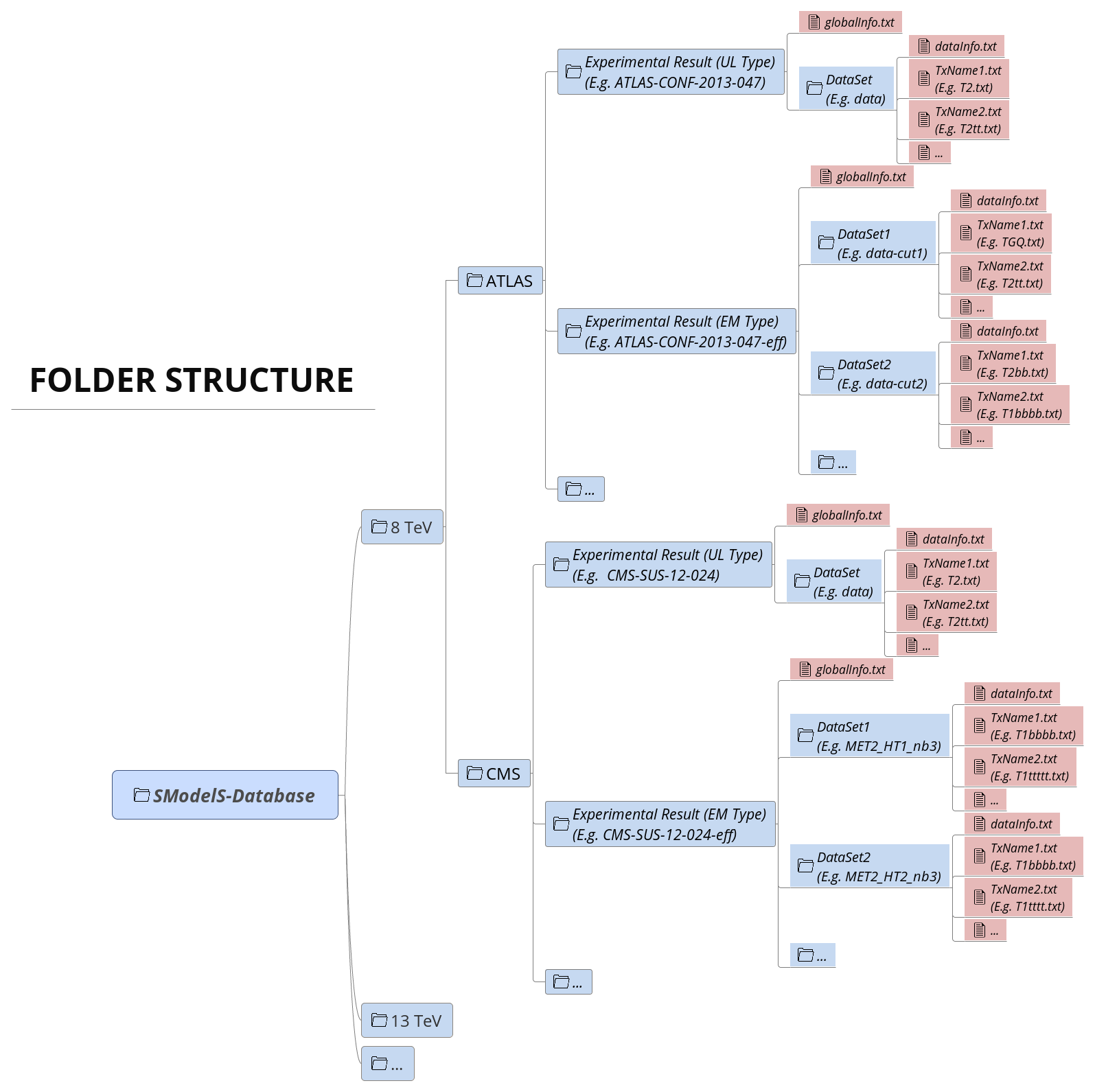
As seen above, the top level of the SModelS database categorizes the analyses by LHC center-of-mass energies, \(\sqrt{s}\):
8 TeV
13 TeV
Also, the top level directory contains a file called version with the
version string of the database.
The second level splits the results up between the different experiments:
8TeV/CMS/
8TeV/ATLAS/
The third level of the directory hierarchy encodes the Experimental Results:
8TeV/CMS/CMS-SUS-12-024
8TeV/ATLAS/ATLAS-CONF-2013-047
…
The Database folder is described by the Database Class
Experimental Result Folder
Each Experimental Result folder contains:
a folder for each DataSet (e.g.
data)a
globalInfo.txtfile
The globalInfo.txt file contains the meta information about the Experimental Result.
It defines the center-of-mass energy \(\sqrt{s}\), the integrated luminosity, the id
used to identify the result and additional information about the source of the
data. Here is the content of CMS-SUS-12-024/globalInfo.txt as an example:
sqrts: 8.0*TeV
lumi: 19.4/fb
id: CMS-SUS-12-024
prettyName: \slash{E}_{T}+b
url: https://twiki.cern.ch/twiki/bin/view/CMSPublic/PhysicsResultsSUS12024
arxiv: http://arxiv.org/abs/1305.2390
publication: http://www.sciencedirect.com/science/article/pii/S0370269313005339
contact: Keith Ulmer <keith.ulmer@cern.ch>, Josh Thompson <joshua.thompson@cern.ch>, Alessandro Gaz <alessandro.gaz@cern.ch>
private: False
implementedBy: Wolfgang Waltenberger
lastUpdate: 2015/5/11
Experimental Result folder is described by the ExpResult Class
globalInfo files are descrived by the Info Class
Data Set Folder
Each DataSet folder (e.g. data) contains:
the Upper Limit maps for UL-type results or Efficiency maps for EM-type results (
TxName.txtfiles)a
dataInfo.txtfile containing meta information about the DataSetData Set folders are described by the DataSet Class
TxName files are described by the TxName Class
dataInfo files are described by the Info Class
Data Set Folder: Upper Limit Type
Since UL-type results have a single dataset (see DataSets), the info file only holds some trivial information, such as the type of Experimental Result (UL) and the dataset id (None for UL-type results). Here is the content of CMS-SUS-12-024/data/dataInfo.txt as an example:
dataType: upperLimit
dataId: None
Data Set Folder: Efficiency Map Type
For EM-type results the dataInfo.txt contains relevant information, such as an id to
identify the DataSet (signal region), the number of observed and expected
background events for the corresponding signal region and the respective signal
upper limits. Here is the content of
CMS-SUS-13-012-eff/3NJet6_1000HT1250_200MHT300/dataInfo.txt as an example:
dataType: efficiencyMap
dataId: 3NJet6_1000HT1250_200MHT300
observedN: 335
expectedBG: 305
bgError: 41
upperLimit: 5.681*fb
expectedUpperLimit: 4.585*fb
TxName Files
Each DataSet contains one or more TxName.txt file storing
the bulk of the experimental result data.
For UL-type results, the TxName file contains the UL maps for a given simplified model
(element or sum of elements), while for EM-type results the file contains
the simplified model efficiencies.
In addition, the TxName files also store some meta information, such
as the source of the data and the type of result (prompt or displaced).
If not specified, the type will be assumed to be prompt.1
For instance, the first few lines of CMS-SUS-12-024/data/T1tttt.txt read:
txName: T1tttt
constraint: [[['t','t']],[['t','t']]]
condition: None
conditionDescription: None
figureUrl: https://twiki.cern.ch/twiki/pub/CMSPublic/PhysicsResultsSUS12024/T1tttt_exclusions_corrected.pdf
source: CMS
validated: True
axes: [[x, y], [x, y]]
As seen above, the first block of data in the file contains information about the element or simplified model ([[[‘t’,’t’]],[[‘t’,’t’]]]) in bracket notation for which the data refers to as well as reference to the original data source and some additional information. The simplified model is assumed to contain neutral BSM final states (MET signature) and arbitrary ( Z2-odd particles) intermediate BSM states. If the experimental result refers to non-MET final states, the finalState field must list the type of BSM particles (see UL-type for more details). An example from the CMS-EXO-12-026/data/THSCPM1b.txt file is shown below:
txName: THSCPM1b
constraint: [[],[]]
source: CMS
axes: [[x], [x]]
finalState: ['HSCP', 'HSCP']
In addition, if specific BSM intermediate states are required, the intermediateState field must include a nested list (one for each branch) specifying the labels of the intermediate BSM states.3 If the intermediateState field is specified, the corresponding result will only be applied to simplified models containing intermediate BSM particles with the same quantum numbers. One example is shown below:
txName: TExample
constraint: [[['q','q'],['W+']],[['q','q'],['W-']]]
finalState: ['MET', 'MET']
intermediateState: [['gluino','C1+'], ['gluino','C1-']]
The second block of data in the TxName.txt file contains the upper limits or efficiencies
as a function of the relevant simplified model parameters:
upperLimits: [[[[4.0000E+02*GeV,0.0000E+00*GeV],[4.0000E+02*GeV,0.0000E+00*GeV]],1.8158E+00*pb],
[[[4.0000E+02*GeV,2.5000E+01*GeV],[4.0000E+02*GeV,2.5000E+01*GeV]],1.8065E+00*pb],
[[[4.0000E+02*GeV,5.0000E+01*GeV],[4.0000E+02*GeV,5.0000E+01*GeV]],2.1393E+00*pb],
[[[4.0000E+02*GeV,7.5000E+01*GeV],[4.0000E+02*GeV,7.5000E+01*GeV]],2.4721E+00*pb],
[[[4.0000E+02*GeV,1.0000E+02*GeV],[4.0000E+02*GeV,1.0000E+02*GeV]],2.9297E+00*pb],
[[[4.0000E+02*GeV,1.2500E+02*GeV],[4.0000E+02*GeV,1.2500E+02*GeV]],3.3874E+00*pb],
[[[4.0000E+02*GeV,1.5000E+02*GeV],[4.0000E+02*GeV,1.5000E+02*GeV]],3.4746E+00*pb],
[[[4.0000E+02*GeV,1.7500E+02*GeV],[4.0000E+02*GeV,1.7500E+02*GeV]],3.5618E+00*pb],
[[[4.2500E+02*GeV,0.0000E+00*GeV],[4.2500E+02*GeV,0.0000E+00*GeV]],1.3188E+00*pb],
[[[4.2500E+02*GeV,2.5000E+01*GeV],[4.2500E+02*GeV,2.5000E+01*GeV]],1.3481E+00*pb],
[[[4.2500E+02*GeV,5.0000E+01*GeV],[4.2500E+02*GeV,5.0000E+01*GeV]],1.7300E+00*pb],
As we can see, the data grid is given as a Python array with the structure: \([[\mbox{masses},\mbox{upper limit}], [\mbox{masses},\mbox{upper limit}],...]\). For prompt analyses, the relevant parameters are usually the BSM masses, since all decays are assumed to be prompt. On the other hand, results for long-lived or meta-stable particles may depend on the BSM widths as well. The width dependence can be easily included through the following generalization:
In order to make the notation more compact, whenever the width dependence is not included, the corresponding decay will be assumed to be prompt and an effective lifetime reweigthing factor will be applied to the upper limits. For instance, a mixed type data grid is also allowed:
The example above represents a simplified model where the decay of the mother is prompt, while the daughter does not have to be stable, hence the dependence on \(\Gamma_2\). In this case, the lifetime reweigthing factor is applied only for the mother decay.
Inclusive Simplified Models
If the analysis signal efficiencies or upper limits are insensitive to some of the simplified model final states, it might be convenient to define inclusive simplified models. A typical case are some of the heavy stable charged particle searches, which only rely on the presence of a non-relativistic charged particle, which leads to an anomalous charged track signature. In this case the signal efficiencies are highly insensitive to the remaining event activity and the corresponding simplified models can be very inclusive. In order to handle this inclusive cases in the database we allow for wildcards when specifying the constraints. For instance, the constraint for the CMS-EXO-13-006 eff/c000/THSCPM3.txt reads:
txName: THSCPM3
constraint: [[['*']],[['*']]]
and represents the (inclusive) simplified model:

Note that although the final state represented by “*” is any Z2-even particle, it must still correspond to a single particle, since the topology specifies a 2-body decay for the initially produced BSM particle. Finally, it might be useful to define even more inclusive simplified models, such as the one in CMS-EXO-13-006 eff/c000/THSCPM4.txt:
txName: THSCPM4
constraint: [[*],[['*']]]
finalState: ['MET', 'HSCP']
In the above case the simplified model corresponds to an HSCP being initially produced in association with any BSM particle which leads to a MET signature. Note that “[*]” corresponds to any branch, while [“*”] means any particle:
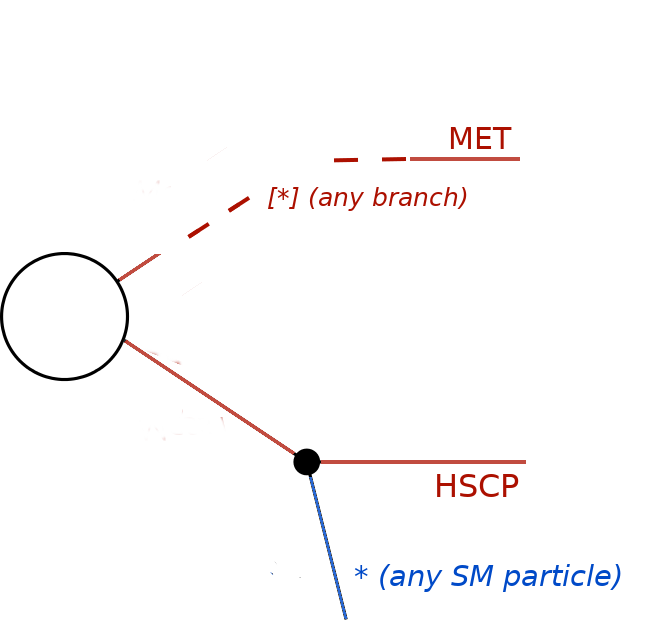
In such cases the mass array for the arbitrary branch must also be specified as using wildcards:
efficiencyMap: [[['*',[5.5000E+01*GeV,5.0000E+01*GeV]],5.27e-06],
[['*',[1.5500E+02*GeV,5.0000E+01*GeV]],1.28e-07],
[['*',[1.5500E+02*GeV,1.0000E+02*GeV]],0.13],
Database: Object Structure
The Database folder structure is mapped to Python objects in SModelS. The mapping is almost one-to-one, with a few exceptions. Below we show the overall object structure as well as the folders/files the objects represent (click to enlarge):
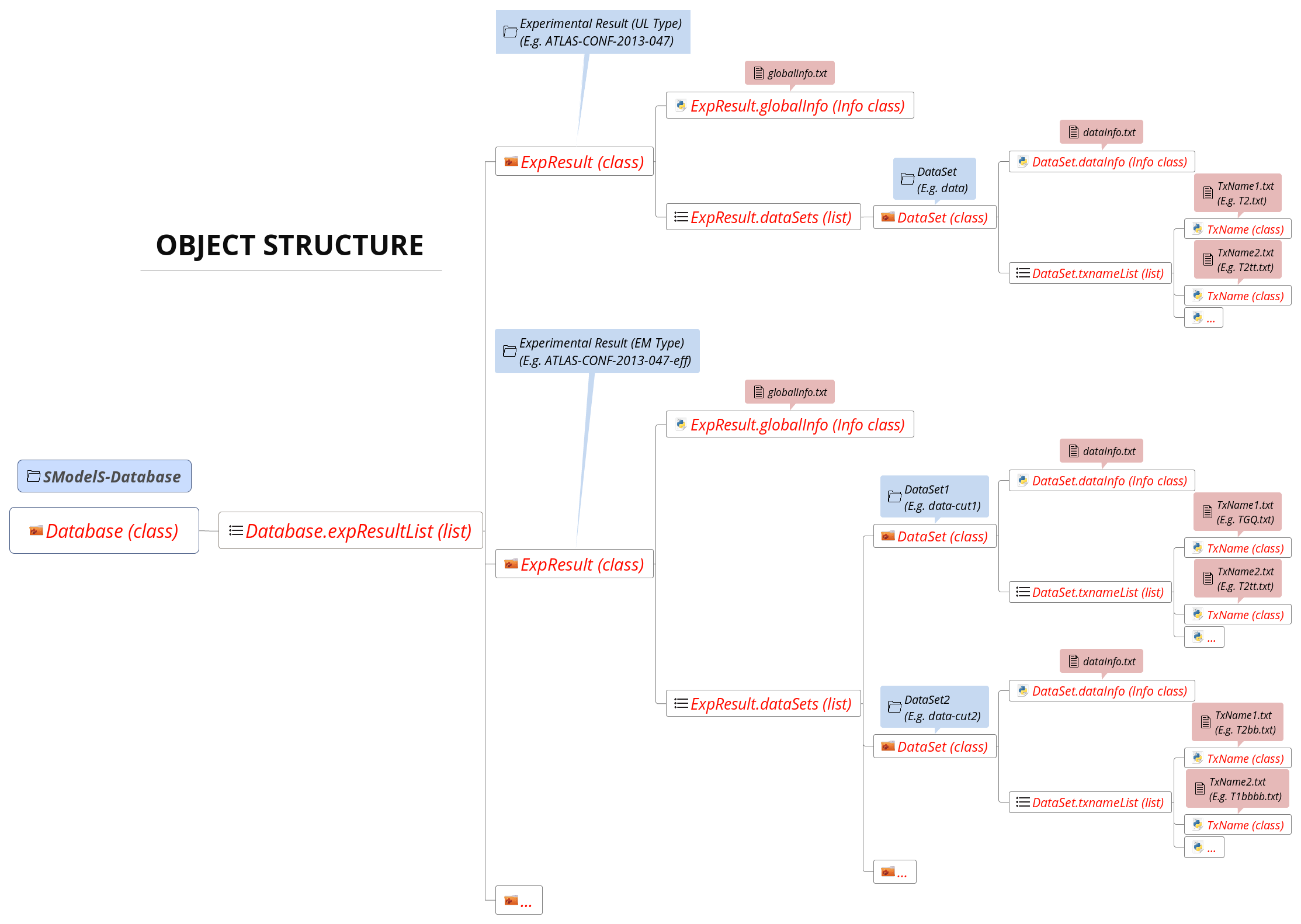
The type of Python object (Python class, Python list,…) is shown in brackets. For convenience, below we explicitly list the main database folders/files and the Python objects they are mapped to:
Database folder \(\rightarrow\) Database Class
Experimental Result folder \(\rightarrow\) ExpResult Class
DataSet folder \(\rightarrow\) DataSet Class
globalInfo.txtfile \(\rightarrow\) Info ClassdataInfo.txtfile \(\rightarrow\) Info ClassTxname.txtfile \(\rightarrow\) TxName Class
Database: Binary (Pickle) Format
At the first time of instantiating the Database class, the text files in <database-path> are loaded and parsed, and the corresponding data objects are built. The efficiency and upper limit maps themselves are subjected to standard preprocessing steps such as a principal component analysis and Delaunay triangulation (see below). For the sake of efficiency, the entire database – including the Delaunay triangulation – is then serialized into a pickle file (<database-path>/database.pcl), which will be read directly the next time the database is loaded. If any changes in the database folder structure are detected, the python or the SModelS version has changed, SModelS will automatically re-build the pickle file. This action may take a few minutes, but it is again performed only once. If desired, the pickling process can be skipped using the option force_load = `txt’ in the constructor of Database .
The pickle file is created by the createBinaryFile method
Database: Data Processing
All the information contained in the database files is stored in the database objects. Within SModelS the information in the Database is mostly used for constraining the simplified models generated by the decomposition of the input model. Each simplified model (or element) generated is compared to the simplified models contrained by the database and specified by the constraint and finalStates entries in the TxName files. The comparison allows to identify which results can be used to test the input model. Once a matching result is found the upper limit or efficiency must be computed for the given input element. As described above, the upper limits or efficiencies are provided as function of masses and widths in the form of a discrete grid. In order to compute values for any given input element, the data has to be processed as decribed below.
The efficiency and upper limit maps are subjected to a few standard preprocessing steps. First all the units are removed, the shape of the grid is stored and the relevant width dependence is identified (see discussion above). Then the masses and widths are transformed into a flat array:
where \(\Gamma_{0} = 10^{-30}\) GeV is a rescaling factor to ensure the log is mapped to large values for the relevant width range.
Finally a principal component analysis and Delaunay triangulation (see figure below) is applied over the new coordinates. The simplices defined during triangulation are then used for linearly interpolating the transformed data grid, thus allowing SModelS to compute efficiencies or upper limits for arbitrary mass and width values (as long as they fall inside the data grid). As seen above, the width parameters are taken logarithmically before interpolation, which effectively corresponds to an exponential interpolation. If the data grid does not explicitly provide a dependence on all the widths (as in the example above), the computed upper limit or efficiency is then reweighted imposing the requirement of prompt decays (see lifetime reweighting for more details). This procedure provides an efficient and numerically robust way of dealing with generic data grids, including arbitrary parametrizations of the mass parameter space, irregular data grids and asymmetric branches.
Lifetime Reweighting
From v2.0 onwards SModelS allows to include width dependent efficiencies and upper limits. However most experimental results do not provide upper limits (or efficiencies) as a function of the BSM particles’ widths, since usually all the decays are assumed to be prompt and the last BSM particle appearing in the cascade decay is assumed to be stable.2 In order to apply these results to models which may contain meta-stable particles, it is possible to approximate the dependence on the widths for the case in which the experimental result requires all BSM decays to be prompt and the last BSM particle to be stable or decay outside the dector. In SModelS this is done through a reweighting factor which corresponds to the fraction of prompt decays (for intermediate states) and decays outside the detector (for final BSM states) for a given set of widths. For instance, asumme an EM-type result only provides efficiencies (\(\epsilon_{prompt}\)) for prompt decays:
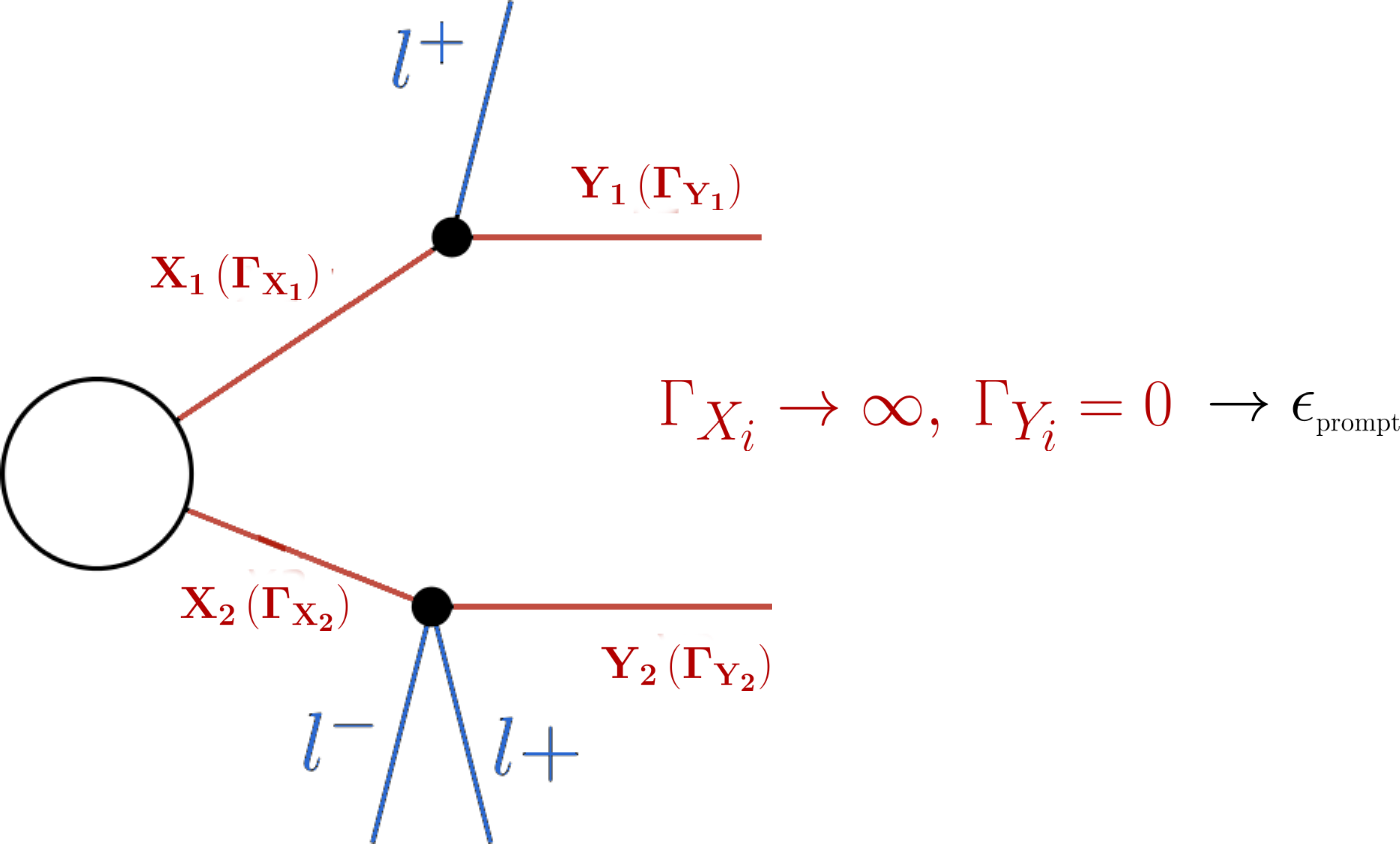
Then, for other values of the widths, an effective efficiency (\(\epsilon_{eff}\)) can be approximated by:
In the expression above \(\mathcal{F}_{prompt}(\Gamma)\) is the probability for the decay to be prompt given a width \(\Gamma\) and \(\mathcal{F}_{long}(\Gamma)\) is the probability for the decay to take place outside the detector. The precise values of \(\mathcal{F}_{prompt}\) and \(\mathcal{F}_{long}\) depend on the relevant detector size (\(L\)), particle mass (\(M\)), boost (\(\beta\)) and width (\(\Gamma\)), thus requiring a Monte Carlo simulation for each input model. Since this is not within the spirit of the simplified model approach, we approximate the prompt and long-lived probabilities by:
where \(L_{outer}\) is the approximate size of the detector (which we take to be 10 m for both ATLAS and CMS), \(L_{inner}\) is the approximate radius of the inner detector (which we take to be 1 mm for both ATLAS and CMS). Finally, we take the effective time dilation factor to be \(\langle \gamma \beta \rangle = 1.3\) when computing \(\mathcal{F}_{prompt}\) and \(\langle \gamma \beta \rangle = 1.43\) when computing \(\mathcal{F}_{long}\). We point out that the above approximations are irrelevant if \(\Gamma\) is very large (\(\mathcal{F}_{prompt} \simeq 1\) and \(\mathcal{F}_{long} \simeq 0\)) or close to zero (\(\mathcal{F}_{prompt} \simeq 0\) and \(\mathcal{F}_{long} \simeq 1\)). Only elements containing particles which have a considerable fraction of displaced decays will be sensitive to the values chosen above. Also, a precise treatment of lifetimes is possible if the experimental result (or a theory group) explicitly provides the efficiencies as a function of the widths, as discussed above.
The above expressions allows the generalization of the efficiencies computed assuming prompt decays to models with meta-stable particles. For UL-type results the same arguments apply with one important distinction. While efficiencies are reduced for displaced decays (\(\xi < 1\)), upper limits are enhanced, since they are roughly inversely proportional to signal efficiencies. Therefore, for UL-type results, we have:
Finally, we point out that for the experimental results which provide efficiencies or upper limits as a function of some (but not all) BSM widths appearing in the simplified model (see the discussion above), the reweighting factor \(\xi\) is computed using only the widths not present in the grid.
- 1
Prompt results are all those which assumes all decays to be prompt and the last BSM particle to be stable (or decay outside the detector). Searches for heavy stable charged particles (HSCPs), for instance, are classified as prompt, since the HSCP is assumed to decay outside the detector. Displaced results on the other hand require at least one decay to take place inside the detector.
- 2
An obvious exception are searches for long-lived particles with displaced decays.
- 3
Although the finalState and intermediateState fields could be combined into a single entry, they are kept separate for backward compatibility.