Decomposition into Simplified Models
Given an input model (see Basic Input), the first task of SModelS is to decompose the full model into a sum of Simplified Models (or elements in SModelS language).
Decomposition
The input model stores information about the masses of all the BSM states as well as their production cross sections, decay branching ratios and total widths. All the cross sections for production of two Z2-odd states serve as the initial step for the decomposition. (All the other cross sections with a different number of Z2-odd states are ignored.) Starting from these primary mothers, all the possible decays are generated according to the decay information for each particle. This procedure is represented in the figure below:
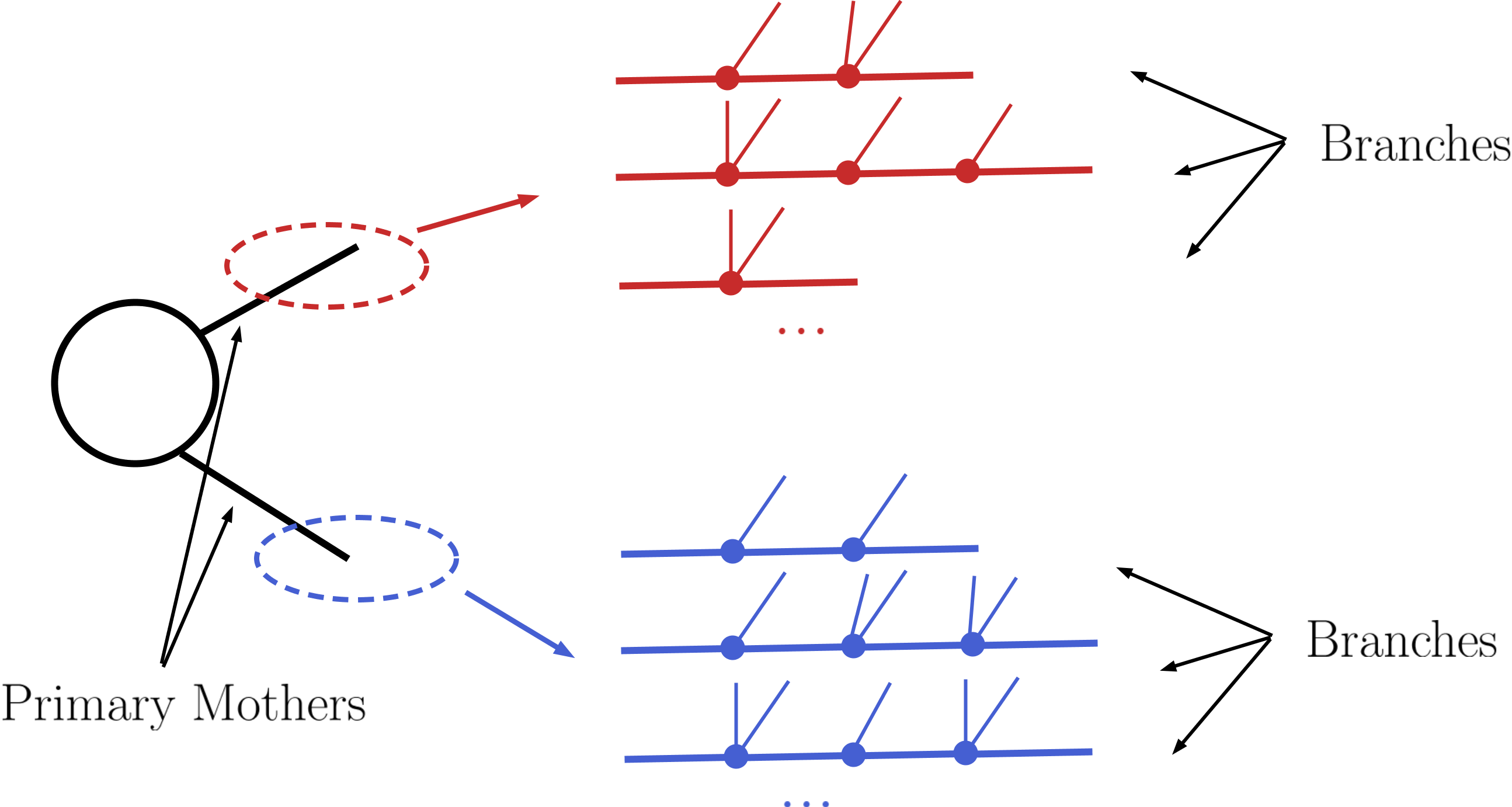
Each of the possible cascade decays for each mother corresponds to a branch. In order to finally generate elements, all the branches are combined in pairs according to the production cross sections, as shown below:
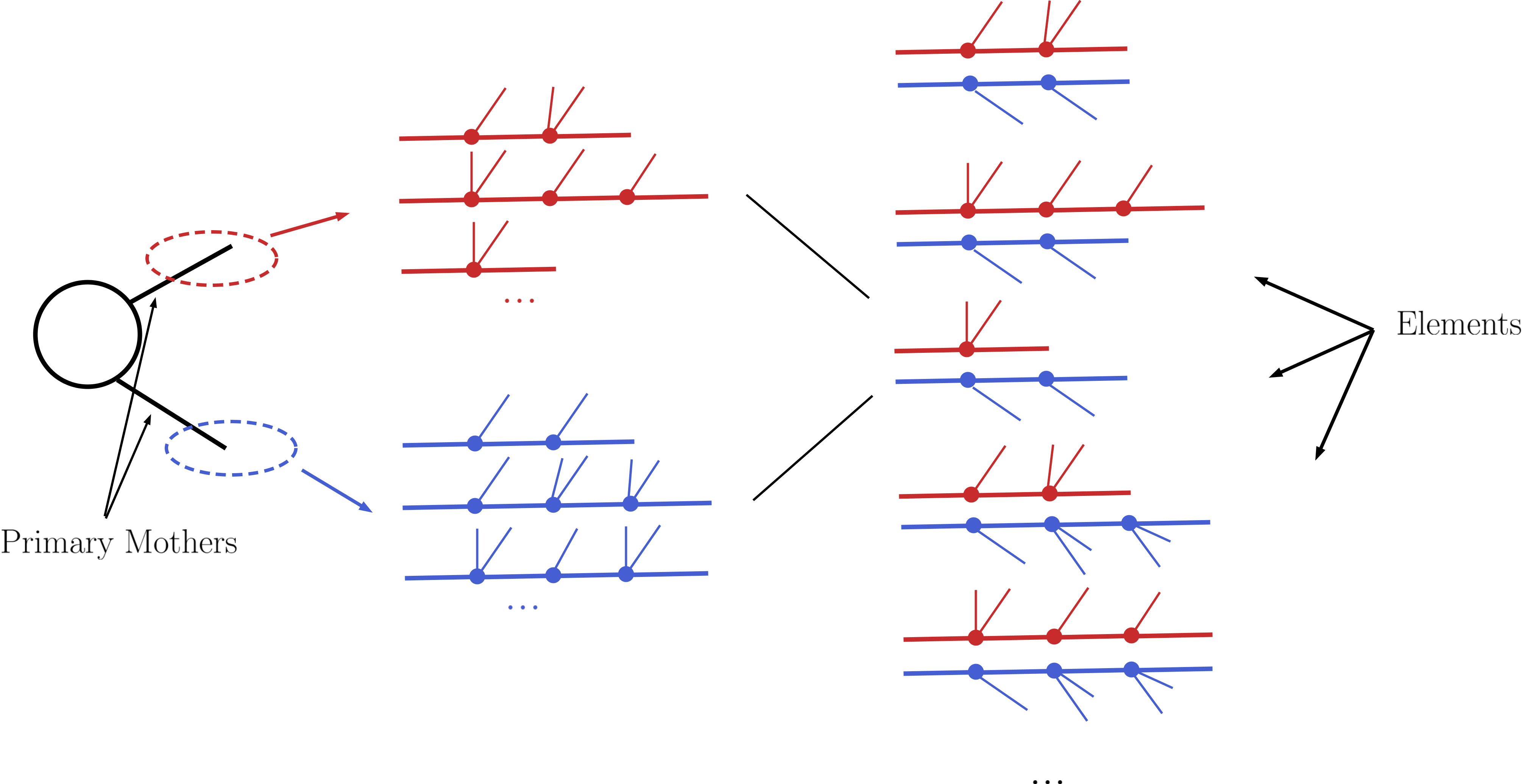
For instance, assume [b1,b2,b3] and [B1,B2] represent all possible branches (or cascade decays) for the primary mothers A and B, respectively. Then, if a production cross section for \(pp \rightarrow A+B\) is given in the input file, the following elements will be generated:
[b1,B1], [b1,B2], [b2,B1], [b2,B2], [b3,B1] and [b3,B2]
The decomposition process either stops when the lightest neutral BSM particle or a stable (or meta-stable) particle is reached. Meta-stable particles are the ones with a total decay width smaller than a certain cutoff value (set by promptWidth in the parameters file). For these states, in addition to the branches where this particle decays, the decomposition will generate branches where this particle appears as a final state (undecayed).
Each of the elements generated according to the procedure just described will also store its weight, which equals its production cross section times all the branching ratios appearing in it. In order to avoid a too large number of elements, only those satisfying a minimum weight requirement are kept. Furthermore, the elements are grouped according to their topologies. The final output of the decomposition is a list of such topologies, where each topology contains a list of the elements generated during the decomposition.
The decomposition is implemented by the decompose method
Minimum Decomposition Weight
Some models may contain a large number of new states and each may have a large number of possible decays. As a result, long cascade decays are possible and the number of elements generated by the decomposition process may become too large, and the computing time too long. For most practical purposes, however, elements with extremely small weights (cross section times BRs) can be discarded, since they will fall well below the experimental limits. Therefore, during the decomposition, whenever an element is generated with a weight below some minimum value, this element (and all elements derived from it) is ignored. The minimum weight to be considered is set by the sigmacut parameter in the parameters file and is easily adjustable (see decomposer.decompose).
Note that, when computing the theory predictions, the weight of several elements can be combined together. Hence it is recommended to set the value of sigmacut approximately one order of magnitude below the minimum signal cross sections the experimental data can constrain.
Compression of Elements
During the decomposition process it is possible to perform several simplifications on the elements generated. Two useful simplifications are possible: Mass Compression and Invisible Compression. The main advantage of performing these compressions is that the simplified element is always shorter (has fewer cascade decay steps), which makes it more likely to be constrained by experimental results. The details behind the compression methods are as follows:
Mass Compression
In case of small mass differences, the prompt decay 1 of a BSM particle to a nearly degenerate one will in most cases produce soft final states, which can not be experimentally detected. Consequently, it is a good approximation to neglect the soft final states and compress the respective decay, as shown below:
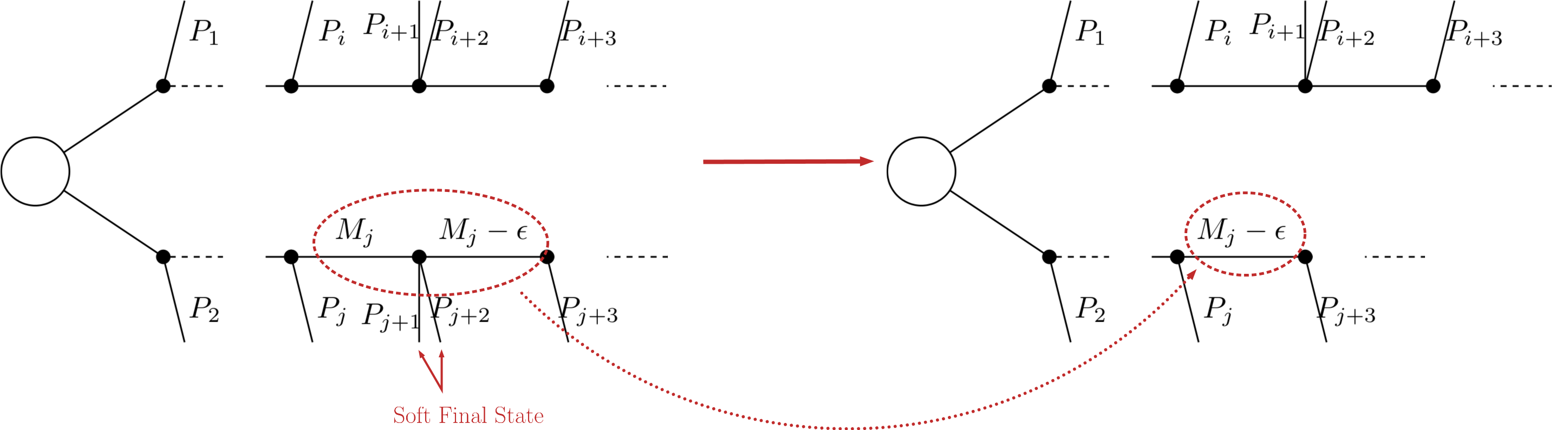
After the compression, only the lightest of the two near-degenerate masses are kept in the element, as shown above. The main parameter which controls the compression is minmassgap, which corresponds to the maximum value of \(\epsilon\) in the figure above to which the compression is performed:
Note that the compression is an approximation since the final states, depending on the boost of the parent state, may not always be soft. It is recommended to choose values of minmassgap between 1-10 GeV; the default value is 5 GeV.
Mass compression is implemented by the massCompress method and can be easily turned on/off by the doCompress parameter in the parameters file.
Invisible Compression
Another type of compression is possible when the last BSM decay appearing in a branch is invisible. The most common example is
as the last step of the decay chain, where \(\nu\) is a SM neutrino, \(A\) is a neutral particle and/or decays promptly and \(B\) is an invisible particle leading to a MET signature. Since both the neutrino and \(B\) are invisible, for all experimental purposes the effective MET object is \(B + \nu = A\). Hence it is possible to omit the last step in the cascade decay, resulting in a compressed element. Note that this compression can be applied consecutively to several steps of the cascade decay if all of them contain only invisible final states:
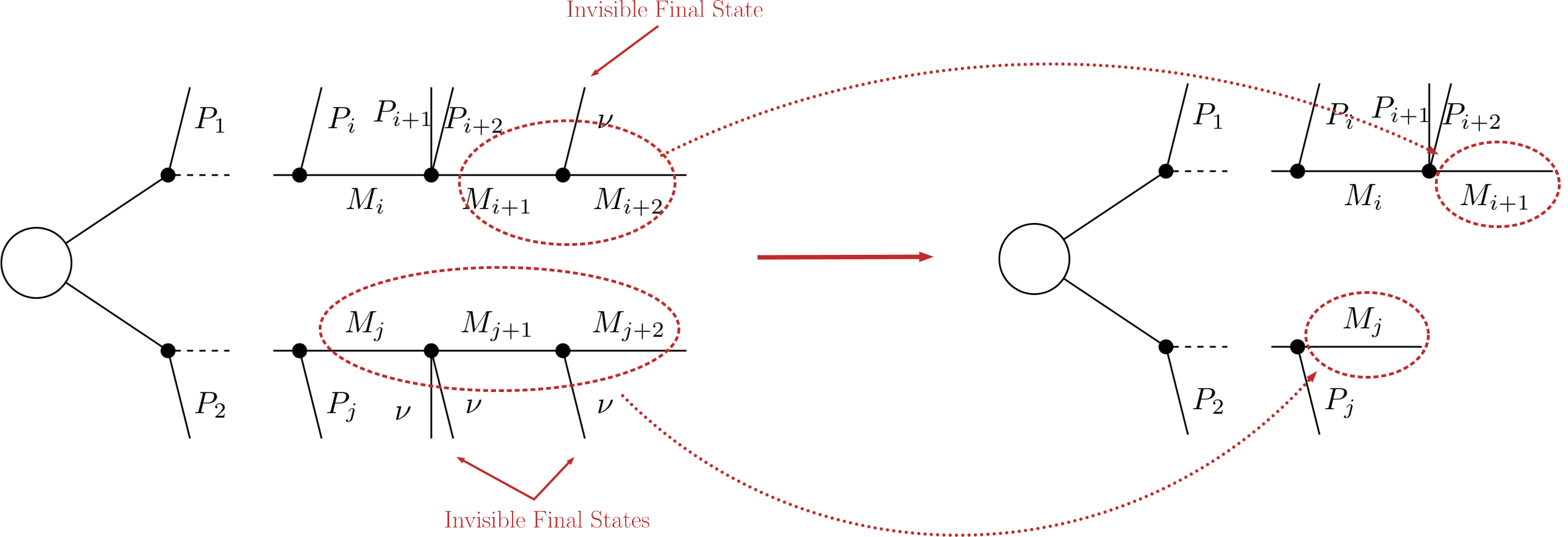
After the compression, the last BSM state appearing in the compressed element is replaced by an effective particle with no electric or color charge, with label “inv” and with the mass of the parent (\(A\) in the example above). Furthermore since the original neutral final state (\(B\)) can in principle be meta-stable, the new effective final state inherits its width.
Invisible compression is implemented by the invisibleCompress method and can be easily turned on/off by the doInvisible parameter in the parameters file.
Element Sorting
In order to improve the code performance, elements created during decomposition and sharing a common topology are sorted. Sorting allows for an convenient ordering of the elements belonging to a topology and faster element comparison. Elements are sorted according to their branches. Branches are compared according to the following order of properties:
Number of vertices
Number of final states in each vertex
BSM (Z2-odd) particles
Z2-even final state particles in each vertex
Finally, particles are compared according to the following order of properties (if defined):
Z2 parity
Spin
Color representation
Electric charge
Mass
Total width
As an example, consider the three elements below where all BSM (Z2-odd) particles only differ by their mass:
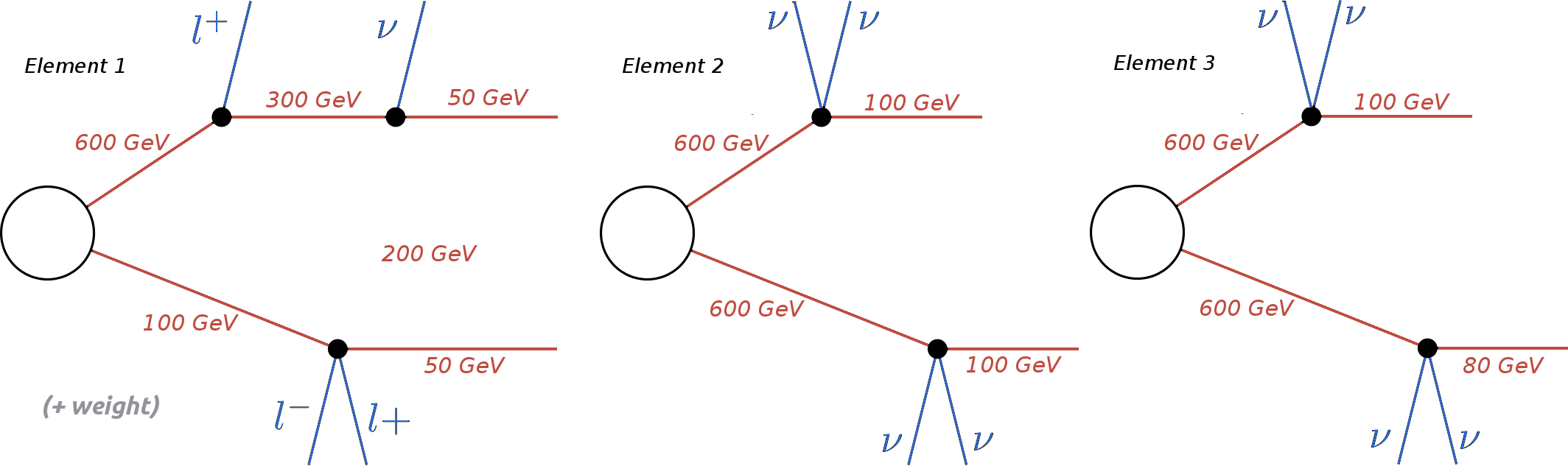
The correct ordering of the above elements is:
Element 3 < Element 2 < Element 1
Element 1 is ‘larger’ than the other two since it has a larger number of vertices. Elements 2 and 3 are identical, except for their masses. Since the last BSM particle appearing in the lower branch of Element 3 has a smaller mass than the corresponding particle in Element 2, the former is ‘smaller’ than the latter. Finally if all the branch features listed above are identical for both branches, the elements being compared are considered to be equal. Futhermore, the branches belonging to the same element are also sorted. Hence, if an element has two branches:
it implies
regarding their ordering.
Branch sorting is implemented by the sortBranches method
- 1
Decays of meta-stable particles should not be compressed, even if soft, since they might result in distinct signatures depending on the quantum numbers of the decaying particle. Particles are assumed to be meta-stable if their width is below the value set by the promptWidth parameter.