Simplified Model Coverage
The constraints provided by SModelS are obviously limited by its database and the available set of simplified model interpretations provided by the experimental collaborations or computed by theory groups. Therefore it is interesting to identify classes of missing simplified models (or missing topologies) which are relevant for a given input model, but are not constrained by the SModelS database. This task is performed as a last step in SModelS, once the decomposition and the theory predictions have been computed.
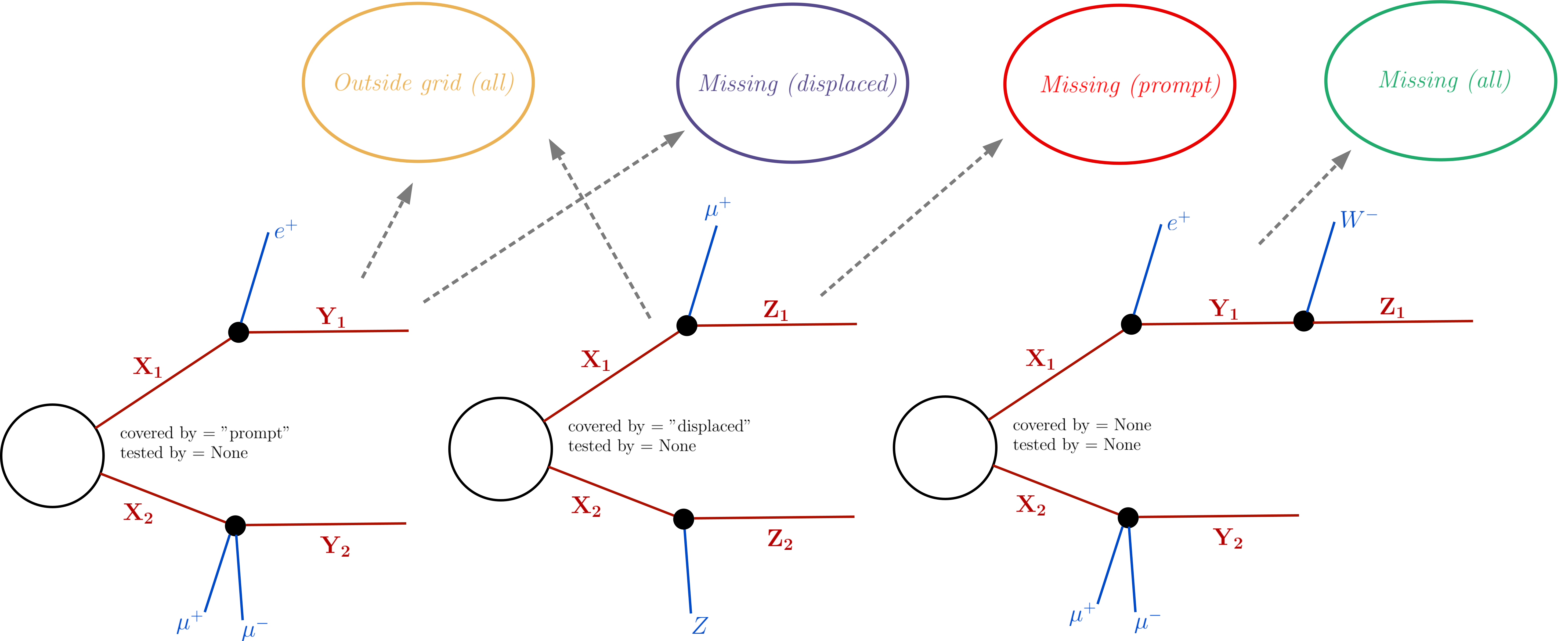
During the computation of the theory predictions, each element from the decomposition which matches at least one of the simplified models in the database is marked as “covered by” the corresponding type of Experimental Result. Currently the Experimental Results are either of type prompt or displaced.1 If the same element is covered by both types of Experimental Results, it will be marked as covered by displaced and prompt results. If, in addition to being covered, the element also has a non-zero efficiency or upper limit (i.e. its properties fall inside the data grid for any result), it will be marked as “tested by” the corresponding type of result (prompt or displaced). Hence, after the theory predictions have been computed, the elements store information about their experimental coverage and can be classified and group into coverage.
The coverage tool is implemented by the Uncovered class
Coverage Groups
The coverage algorithm groups all the elements into coverage groups which can be easily defined by the user (see the coverage module). Each group must define a criterium for selecting elements after the theory predictions have been computed. The default coverage groups implemented in SModelS are:
missing (prompt): not covered by prompt-type results. This group corresponds to all elements which did not match any of the simplified models contrained by prompt Experimental Results.
missing (displaced): not covered by displaced-type results. This group corresponds to all elements which did not match any of the simplified models contrained by displaced Experimental Results.
missing (all): not covered by any type of result. This group corresponds to all elements which did not match any of the simplified models contrained by the database.
outsideGrid (all): covered by at least one type of Experimental Result and not tested by any type of result. This group corresponds to all elements which matched at least one the simplified models constrained by the database, but were not tested (e.g. their masses and/or widths fall outside the efficiency or upper limit grids).
The figure below schematically represents the grouping performed in coverage:
Besides defining which elements should be selected, each coverage group can also specify a reweighting function for the element’s cross section. This is useful for the cases where the coverage group aims to represent missing topologies with prompt (or displaced) decays, so only the fraction of prompt (displaced) cross section should be extracted. The reweighting functions defined will be applied to the selected elements in order to extract the desirable fraction of signal cross section for the group. For instance, for the default groups listed above, the following reweighint functions are defined:
missing (prompt): \(\sigma \to \xi \times \sigma,\;\; \xi = \prod_{i=1,N-2} \mathcal{F}_{prompt}^{i} \times \prod_{i=N-2,N} \mathcal{F}_{long}^{i}\)
missing (displaced): \(\sigma \to \xi \times \sigma,\;\; \xi = \mathcal{F}_{displaced}(any) \times \prod_{i=N-2,N} \mathcal{F}_{long}^{i}\)
missing (all): \(\sigma \to \xi \times \sigma,\;\; \xi = 1\)
outsideGrid (all): \(\sigma \to \xi \times \sigma,\;\; \xi = 1\)
The definition for the fraction of long-lived (\(\mathcal{F}_{long}\)) and prompt (\(\mathcal{F}_{prompt}\)) decays can be found in lifetime reweighting. The fraction \(\mathcal{F}_{displaced}(any)\) corresponds to the probability of at least one displaced decay taking place, where the probability for a displaced decay is given by \(1-\mathcal{F}_{long}-\mathcal{F}_{prompt}\).
If mass or invisible compression are turned on, elements generated by compression and their ancestors (original/uncompressed element) could both fall into the same coverage group. Since the total missed cross section in a given group should equal the total signal cross section not covered or tested by the corresponding type of Experimental Results, one has to avoid double counting elements. In addition, a compressed element belonging to a given coverage group could combine cross sections from more than one uncompressed (original) element. If one of the original elements do not belong to this coverage group (i.e. it has been covered and/or tested by the Experimental Results), its contribution to the compressed element cross section should be subtracted. SModelS deals with the above issues through the following steps:
an effective “missing cross section” is computed for each element, which corresponds to the element weight subtracted of the weight of its ancestors which do not belong to the same coverage group. The effective cross section also includes the reweighting discussed above.
All elements belonging to the same group which have a common ancestor are removed (only the element with largest missing cross section is kept).
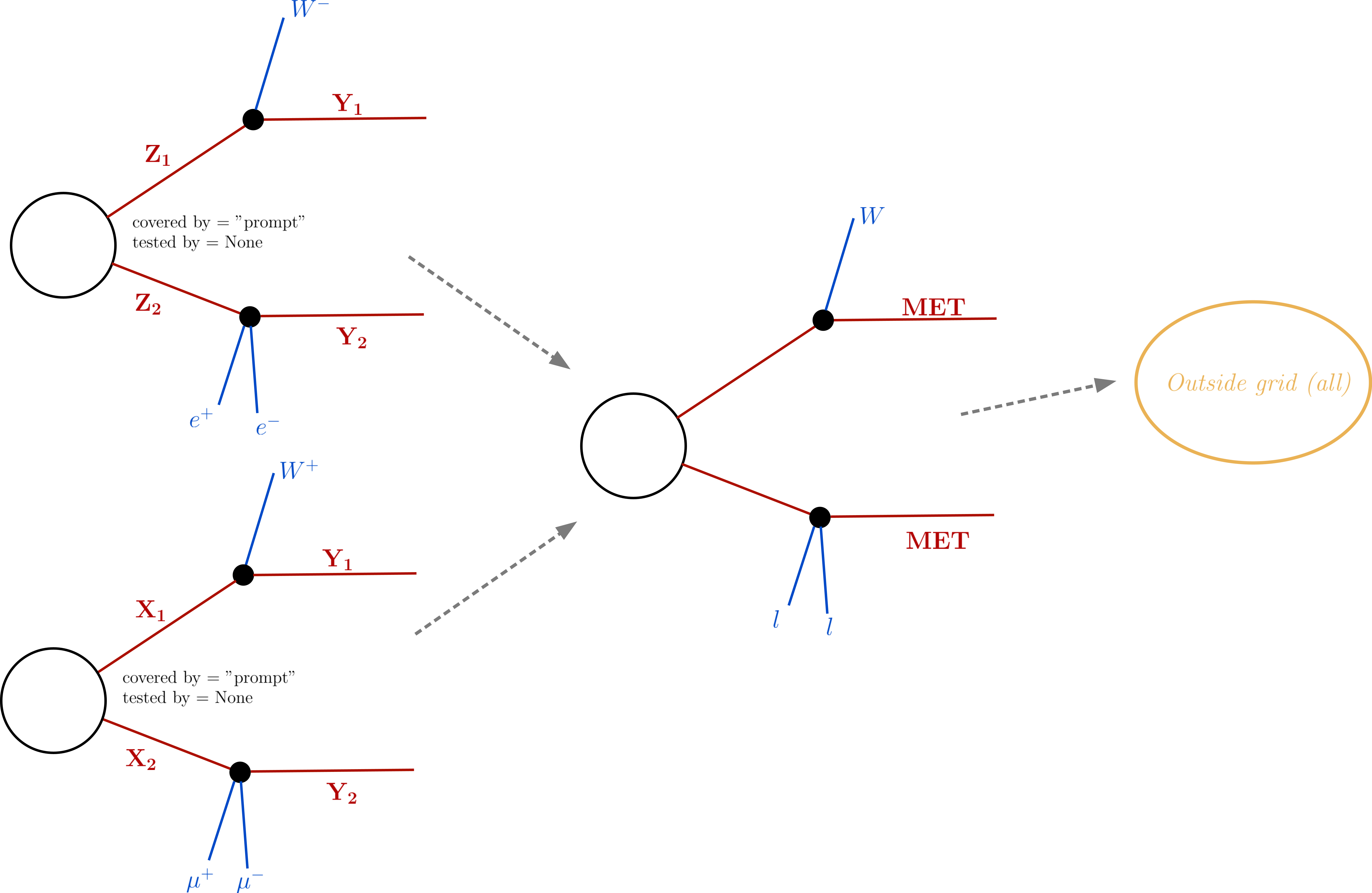
Usually the list of elements in each group can be considerably long, due to distinct intermediate BSM states and final SM states. In order to make the list more compact, all elements are further combined according to their topology and final state particles (i.e. all properties of intermediate BSM states are ignored). By default, the SM particles are grouped according to the definitions below:
\(W^+,W^- \to \mbox{W}\)
\(\tau^+,\tau^- \to \mbox{ta}\)
\(e^+,e^-,\mu^+,\mu^- \to \mbox{l}\)
\(t,\bar{t} \to \mbox{t}\)
\(u,d,s,c,\bar{u},\bar{d},\bar{s},\bar{c},g,pions \to \mbox{jet}\)
\(\nu_{e},\nu_{\mu},\nu_{\tau},\bar{\nu}_{e},\bar{\nu}_{\mu},\bar{\nu}_{\tau} \to \mbox{nu}\)
while the final ( Z2-odd) BSM particles are grouped by their signature:
color and electrically neutral states \(\to \mbox{MET}\)
color neutral states with electric charge +-1 \(\to \mbox{HSCP}\)
color triplet states with electric charge +-2/3 or +-1/3 \(\to \mbox{RHadronQ}\)
color octates states with zero electric charge \(\to \mbox{RHadronG}\)
The figure below schematically represents the combination of elements according to the grouping of similar final states:
Coverage groups are implemented by the UncoveredGroup class
- 1
Prompt results are all those which assumes all decays to be prompt and the last BSM particle to be stable (or decay outside the detector). Searches for heavy stable charged particles (HSCPs), for instance, are classified as prompt, since the HSCP is assumed to decay outside the detector. Displaced results on the other hand require at least one decay to take place inside the detector.